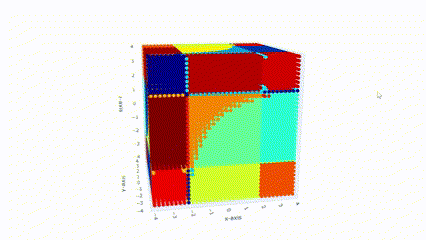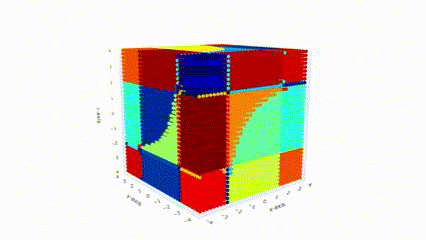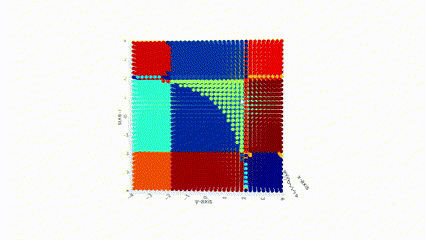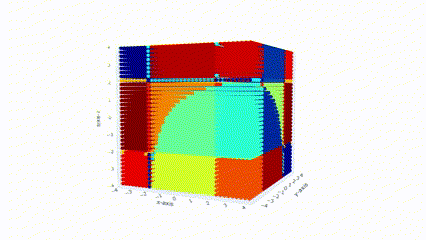
I am interested in geometry of a space of totally non-degenerate real quadratic forms. They are local models of ridgy Lagrangians introduced as a tool in the arborealization program. There is an equivalent notion of principally regular matrices i.e. a space of real symmetric matrices all whose principal minors are non-zero.

I formulated the conjecture that every connected component of the space is contractible. Studying semialgebraic sets that are given via the sign pattern assignments to all principal minors is equivalent to studying orientations on the uniform-oriented Lagrangian matroid.

I am interested in exploring the connection between Deep Polynomial Neural Networks and Tensor Decomposition.
I am fascinated with algebra of neural networks, thinking about the topology of the image of parameter space inside the model space. Also, it leads to some thoughts about the landscape of a loss function during the training process. One of the main goal is to get a better understanding of these well described neural networks and, possibly, jump on CNN networks and other architectures.

For example, shallow polynomial networks with a single output has a space of homogeneous polynomials as a model space and training that network is equivalent to finding a symmetric CP-rank approximation of a given symmetric tensor.

I am also interested in thinking about applications of Direction 1 and 2 in algebraic statistics (Determinantal Point Process, Directed Graphical Models) and in non-convex optimization (a landscape of a loss function).

One of the main sources of my inspiration and motivation is to do numerical experiments.

For Direction I, I generate a point cloud approximation of each connected component and study its topology using ripser i.e. persistent homology. I worked with a point cloud of sizes up to a million points which brings its challenges. I use Lawrence Berkeley National Laboratory clusters to do my computation in Python and C++.

For Direction II, I have constructed polynomial neural networks of different architectures to observe computationally my theoretical findings and to experiment with certain architectures to make conjectures or understand the geometry and behavior of neural network architectures.

For Direction III, I use homotopy continuation to count the number of critical points for the log likelihood function and a combination of persistence homology and principal component analysis to understand a landcsape of a loss function and behavior of a neural network during training process.

Date	Title	Location
2024 January	"Likelihood Geometry of Determinantal Point Processes"	JMM
2023 Fall	"Polynomial Neural Networks"	IMSI
2018 January	"Chromatic Graph Homology for Brace Algebras"	JMM

Date	Title	Location
2024 Winter	"Geometry of Deep Polynomial Neural Networks"	UC Berkeley, Math and ML Seminar
2024 Winter	"Geometry of Principally Regular Matrices"	UBC, IAM Seminar
2023 Fall	"Geometry of Principally Regular Matrices"	SFSU, AGC Seminar
2023 Fall	"Polynomial Neural Networks"	UC Berkeley, Computational Math Seminar
2023 Summer	"Topology of the Complement of Determinantal Variety"	Leipzig University
2021 Fall	"Applications of Riemann-Roch theorem"	UC Berkeley, Student Algebraic Curve Seminar
2021 Spring	"Hochschild Homology and differential forms"	UC Irvine, Graduate Algebra Seminar
2019 Fall	"Colored Jones Polynomials"	UC Berkeley, Student Topology Seminar
2019 Spring	"Hyperbolic Dehn Surgeries"	UC Berkeley, Student Topology Seminar
2017 Spring	"Homotopy Algebras: A-infinity, E2, and Brace"	UC Irvine, Graduate Algebra Seminar
2017 Spring	"Preliminaries on Knot Theory: Jones Polynomials and Vassiliev Invariant"	UC Irvine, Undergraduate Math Club