Research

I am interested in questions at the intersection of Algebraic Geometry and Machine Learning. More concretely, I am interested in how to apply algebro-geometric tools to learn the underlying structure of real-world data through neural networks.
 

• In Machine Learning, I am studying neural network expressivity through the lens of a neuromanifold, a finite-dimensional embedding of a fixed architecture into the ambient space. Understanding the geometry of the neuromanifold provides insights into how and why neural networks train and behave.

  • Another direction of my work concerns neural network quantization, approached via reduced weight precision and pruning.

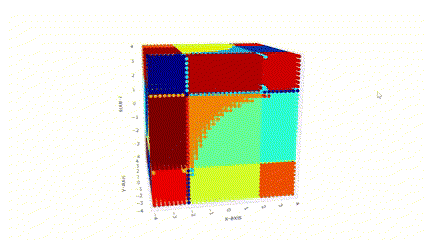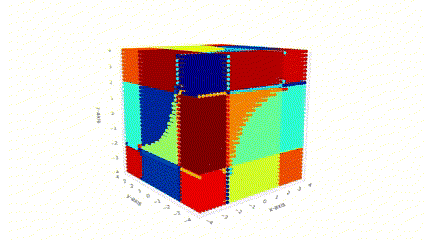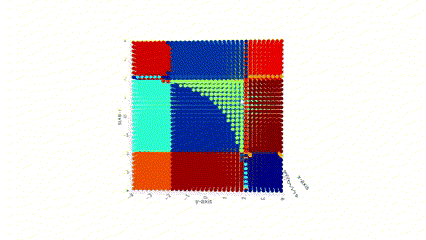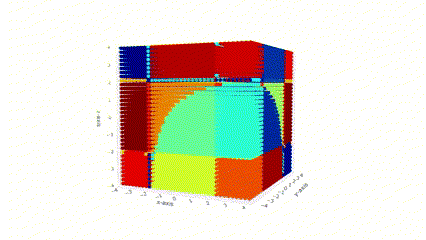
• In Algebraic Geometry, I am interested in studying simultaneous (and other) tensor decompositions, which correspond to various polynomial/rational neural network architectures.

  • Another line of my research focuses on using neural networks to identify the location and type of singularities of meromorphic functions from data.

Here is my CV.